Predefinição:Quadro negro

Documentação da predefinição[ver] [editar] [histórico] [purgar]

Descrição

A predefinição Quadro negro é um modelo para a apresentação de conteúdos extensos de relevância secundária em artigos. Permite a apresentação completa desses conteúdos extensos sem sobrecarregar e congestionar o artigo, equilibrando o destaque, a ocupação e acesso ao artigo e ao conteúdo extenso. Permite ainda a exploração desse conteúdo com o uso das barras de navegação e permite durante a edição o ajuste das dimensões da janela. Por conteúdo extenso como exemplificação citamos: Listas, cálculos, cronologias, figuras entre outros. A atual versão não permite o uso com tabelas transcluídas, as tabelas devem ser referenciadas como Predefinição.

{{{Aviso}}}

{{{Título}}}

{{{título_01}}}

Quadro negro {{{texto_01}}}

{{{título_02}}}

Quadro negro {{{texto_02}}}

Uso

O conteúdo apresentado pode usar o formato básico da predefinição ou ser personalizado dentro das linhas da tabela. A estrutura da predefinição é formada por uma linha de aviso externa, por um título interno e por quadros com pares de rótulo/dados. Estes dados podem ser de qualquer natureza, como textos, imagens, ou até mesmo outras predefinições. O formato básico é apresentado logo abaixo, e outros exemplos práticos são mostradas na seção correspondente.

Estrutura de edição do formato básico {{Predefinição:Quadro negro <!-- Nota de aviso e título destacado --> |altura = altura |largura = largura |cor fundo = cor fundo |cor borda = cor borda |aviso_01 = Aviso |cor subquadro_00 = cor de fundo |título_00 = título <!--- Quadros com sub-título e conteúdo ---> |cor subquadro_01 = cor de fundo |título_01 = sub-título |texto_01 = texto |cor subquadro_02 = cor de fundo |título_02 = sub-título |texto_02 = texto }}

Uso com imagem

A imagem pode ser adicionada da seguinte forma [[Ficheiro:nome do ficheiro da imagem|outros parâmetros]]. Os outros parâmetros são os usuais para a utilização de figuras. A predefinição predefinição Superimpose2: é também uma boa opção para figuras(Infográficos) com marcadores ou pares fundo/texto, ver exemplo no tópico abaixo.

Estrutura de edição do formato básico {{Predefinição:Quadro negro <!-- Nota de aviso e título destacado --> |altura = altura |largura = largura |cor fundo = cor fundo |cor borda = cor borda |aviso_01 = Aviso |cor subquadro_00 = cor de fundo |título_00 = título <!--- Quadros com sub-título e conteúdo ---> |cor subquadro_01 = cor de fundo |título_01 = sub-título |texto_01 = [[Ficheiro:imagem]] texto }}

Exemplos

Quadro negro de textos

Exemplo simples de uso com lista referenciada como predefinição:

Lista exemplo: Lista das espécies de Theraphosidae

A figura abaixo mostra a Lista das espécies de Theraphosidae. Use a barra de rolagem à direita para navegar:

Lista das espécies de Theraphosidae

Theraphosidae

Predefinição:Lista das espécies de Theraphosidae

Quadro negro de cálculos

Exemplo de uso com cálculos (texto formatado) transcluídos:

Cálculo exemplo: Anexo:Exemplos de cálculos da densidade do ar

Conteúdo integral do anexo atualizado em 28/04/2014

A figura abaixo mostra exemplos de cálculo da densidade do ar; para navegar nas folhas de cálculo use a barra de rolagem à direita.

1.0 Cálculos da densidade do ar

1.1 - Temperatura e pressão ( Cálculo da densidade do ar seco )

A densidade do ar seco pode ser calculada usando a lei dos gases ideais, expressa como função da temperatura e da pressão: <math> \rho = \frac{p}{R_{\rm especifico} T} </math>      (Equação 1.1) para: <math>p =</math> pressão absoluta, <math>101,325kPa</math> convertendo em unidades consistentes com a equação, de <math>kPa</math> para <math>Pa</math> <math>p =</math> pressão absoluta, <math>101325 Pa</math> <math>T =</math> temperatura absoluta, <math>(273,15+20^\circ C).K</math> <math>R_{\rm especifico} =</math> constante específica do gás para o ar seco, <math>287,058 J.kg^{-1}.K^{-1}</math> substituindo: <math> \rho = \frac{101325 Pa}{287,058 J.kg^{-1}.K^{-1}.293,15 K} </math>      (Cálculo 1.1) a densidade do ar fica: <math>\rho = 1,204 kg.m^{-3} </math>      (Resultado 1.1)

1.2 - Umidade ( Cálculo da densidade do ar úmido )

A densidade do ar úmido pode ser calculada como uma mistura de gases ideais. Nesse caso, a pressão parcial do vapor d'água é denominada pressão de vapor. Usando este método, o erro no cálculo da densidade é menor que 0.2% no intervalo de −10 °C a 50 °C. A densidade é obtida por: <math> \rho_{\,\mathrm{ar~umido

= \frac{p_{d}}{R_{d} T} + \frac{p_{v}}{R_{v} T}

</math>      (Equação 1.2) ,ou

<math>

\rho_{\,\mathrm{ar~umido}} = \frac{p_{d}M_{d}+p_{v}M_{v}}{R T} \, </math>      (Equação 1.2) ,outra forma.

para:

<math>p_{d} =</math> Pressão parcial do ar seco, <math>100,155953 kPa</math> (calculado abaixo por 1.2.3)

convertendo em unidades consistentes com a equação, de <math>kPa</math> para <math>Pa</math>

<math>p_{d} =</math> Pressão parcial do ar seco, <math>100155,953 Pa</math>

<math>R_{d} =</math> Constante específica do gás para o ar seco, <math>287,058 J.kg^{-1}.K^{-1}</math>

<math>T =</math> temperatura absoluta, <math>(273,15+20^\circ C).K</math>

<math>p_{v} =</math> Pressão do vapor d'água, <math>1,169047 kPa</math> (calculado abaixo por 1.2.1)

convertendo em unidades consistentes com a equação, de <math>kPa</math> para <math>Pa</math>

<math>p_{v} =</math> Pressão do vapor d'água, <math>1169,047 Pa</math>

<math>R_{v} =</math> Constante específica do gás para o vapor d'água, <math>461,495 J.kg^{-1}.K^{-1}</math>

<math>M_{d} =</math> Massa molar do ar seco, <math>0,028964 kg.mol^{-1}</math>

<math>M_{v} =</math> Massa molar do vapor d'água, <math>0,018016 kg.mol^{-1}</math>

<math>R =</math> Constante do gás ideal, <math>8,314 J.K^{-1}mol^{-1})</math>

substituindo:

<math>

\rho_{\,\mathrm{ar~umido}} = \frac{100156 Pa}{287,058 J.kg^{-1}.K^{-1}.293,15K} + \frac{1169 Pa}{461,495 J.kg^{-1}.K^{-1}.293,15K} \, </math>    (Cálculo 1.2) ,ou

<math>

\rho_{\,\mathrm{ar~umido}} = \frac{100156 Pa.0,028964 kg.mol^{-1}+1169 Pa.0,018016 kg.mol^{-1}}{8,314 J.K^{-1}mol^{-1}.293,15 K} \, </math>      (Cálculo 1.2) ,outra forma.

a densidade do ar úmido fica:

<math>\rho_{\,\mathrm{ar~umido}} = 1,1988 kg.m^{-3}

</math>      (Resultado 1.2)

Nota:

• A diferença entre os dois cálculos abaixo do valor de <math>1,1988\left(nn\cdots\right)</math> se deve aos arredondamentos utilizados.

|cor subquadro_03 = #dcdcff |título_03 = 1.2.1 - Umidade ( Cálculo da pressão parcial do vapor da água ) |texto_03 =

A pressão de vapor da água pode ser calculada pela pressão de saturação do vapor e a umidade relativa, sendo obtida por:

<math>

p_{v} = \phi p_{\mathrm{sat}} \, </math>      (Equação 1.2.1)

para:

<math>\phi =</math> Umidade relativa, <math>50\%</math>

<math>p_{\mathrm{sat}} =</math> Pressão de saturação do vapor, <math>2,338094 kPa</math> (calculado abaixo por 1.2.2)

substituindo:

<math>

p_{v} = 50\%.2,338094 kPa \, </math>      (Cálculo 1.2.1)

<math>p_{v} =</math> Pressão de vapor da água

a pressão de vapor da água fica:

<math>p_{v} = 1,169047 kPa

</math>      (Resultado 1.2.1)

|cor subquadro_04 = #dcdcff |título_04 = 1.2.2 - Umidade ( Cálculo da pressão de saturação do vapor da água ) |texto_04 =

A pressão de saturação de vapor d'água em qualquer temperatura é a pressão de vapor quando a umidade relativa é de 100%.

Uma equação usada para obter a pressão de saturação do vapor é:

<math>p_{\mathrm{sat}} = 6,1078 \times 10^{\frac{7,5 T}{T+237,3}} \,

</math>      (Equação 1.2.2)

onde <math>T =</math> é em graus C.

para:

<math>T =</math> temperatura, <math>20^\circ C</math>

substituindo:

<math>p_{\mathrm{sat}} = 6,1078 \times 10^{\frac{7,5{.}20^\circ C}{20^\circ C+237,3}} \,

</math>      (Equação 1.2.2)

a pressão de saturação do vapor fica:

<math>p_{\mathrm{sat}} = 23,38094 hPa (milibar)

</math>

ou <math>p_{\mathrm{sat}} = 2,338094 kPa

</math>      (Resultado 1.2.2)

Nota:

• Este resultado da equação dará a pressão em hPa (100 Pa, equivalente a unidade em desuso milibar, 1 mbar = 0,001 bar = 0,1 kPa)

|cor subquadro_05 = #dcdcff |título_05 = 1.2.3 - Umidade ( Cálculo da pressão parcial do ar seco ) |texto_05 =

A pressão parcial do ar seco <math>p_{d}</math> é obtida considerando a pressão parcial, resultando em:

<math>

p_{d} = p-p_{v} \, </math>      (Equação 1.2.3)

Onde <math>p</math> simplesmente denota o valor observado da pressão absoluta.

para:

<math>p =</math> Pressão absoluta local, <math>101,325 kPa</math>

<math>p_{v} =</math> Pressão do vapor d'água, <math>1,169047 kPa</math> (calculado acima por 1.2.1)

substituindo:

<math>

p_{d} = 101,325 kPa-1,169047 kPa \, </math>      (Cálculo 1.2.3)

a pressão parcial do ar seco fica:

<math>p_{d} = 100,155953 kPa

</math>      (Resultado 1.2.3)

|cor subquadro_06 = #ccccff |título_06 = 1.3 - Altitude ( Cálculo da densidade em função da Altitude ) |texto_06 = Para calcular a densidade do ar em função da altitude, são necessários os parâmetros listados abaixo, juntamente com os seus valores de acordo com a Atmosfera padrão internacional, utilizando no cálculo a constante de gás universal no lugar da constante específica do ar:

A densidade pode ser calculada de acordo com a equação molar da lei do gás ideal:

<math>

\rho = \frac{p M}{R T} \, </math>      (Equação 1.3)

para:

<math>h =</math> altitude, <math>5000 m</math>

<math>p =</math> pressão atmosférica absoluta, <math>49,587 kPa</math> (calculado abaixo por 1.3.2)

convertendo em unidades consistentes com a equação, de <math>kPa</math> para <math>Pa</math>

<math>p =</math> pressão atmosférica absoluta, <math>49587,0 Pa</math>

<math>T =</math> temperatura atmosférica, <math>255,65 K</math> (calculado abaixo por 1.3.1)

<math>R =</math> constante do gás ideal, <math>8,31447 J.mol^{-1}.K^{-1}</math>

<math>M =</math> massa molar do ar seco, <math>0,0289644 kg.mol^{-1}</math>

substituindo:

<math>

\rho = \frac{49587,0 Pa.0,0289644 kg.mol^{-1}}{8,31447 J.mol^{-1}.K^{-1} 255,65 K} \, </math>      (Cálculo 1.3)

a densidade do ar fica:

<math>\rho = 0,676 kg.m^{-3}

</math>      (Resultado 1.3)

|cor subquadro_07 = #dcdcff |título_07 = 1.3.1 - Altitude ( Cálculo da temperatura em função da Altitude ) |texto_07 = A temperatura na altitude <math>h</math> em metros acima do nível do mar é aproximada pela seguinte fórmula (somente válida dentro da troposfera)

<math>

T = T_0 - L h \, </math>      (Equação 1.3.1)

para:

<math>h =</math> altitude, <math>5000 m</math>

<math>T_0 =</math> temperatura atmosférica padrão ao nível do mar, <math>288,15 K</math>

<math>L =</math> taxa de gradiente adiabático, <math>0,0065 K.m</math>

substituindo:

<math>

T = T_0 - L h \, </math>      (Cálculo 1.3.1)

a temperatura do ar fica:

<math>T = 255,65 K

</math>      (Resultado 1.3.1)

|cor subquadro_08 = #dcdcff |título_08 = 1.3.2 - Altitude ( Cálculo da pressão em função da Altitude ) |texto_08 = A pressão a uma altitude <math>h</math> em metros é obtida por:

<math>p = p_0 \left(1 - \frac{L h}{T_0} \right)^\frac{g M}{R L} \,

</math>      (Equação 1.3.2)

para:

<math>h =</math> altitude, <math>5000 m</math>

<math>p_0 =</math> pressão atmosférica padrão ao nível do mar, <math>101,325 kPa</math>

<math>T_0 =</math> temperatura atmosférica padrão ao nível do mar, <math>288,15 K</math>

<math>g =</math> aceleração da gravidade ao nível do solo, <math>9,80665 m.s^{-2}</math>

<math>L =</math> taxa de gradiente adiabático, <math>0,0065 K.m</math>

<math>R =</math> constante do gás ideal, <math>8,31447 J.mol^{-1}.K^{-1}</math>

<math>M =</math> massa molar do ar seco, <math>0,0289644 kg.mol^{-1}</math>

substituindo:

<math>p = 101,325 kPa \left(1 - \frac{0,0065 K.m.5000 m}{288,15 K} \right)^ \left(\frac{9,80665 m.s^{-2}.0,0289644 kg.mol^{-1}}{8,31447 J.mol^{-1}.K^{-1}.0,0065 K.m} \right) \,

</math>      (Cálculo 1.3.2)

a pressão do ar fica:

<math>p = 49,587 kPa

</math>      (Resultado 1.3.2)

}}

Quadro negro de imagem

Exemplo de uso com imagem vertical:

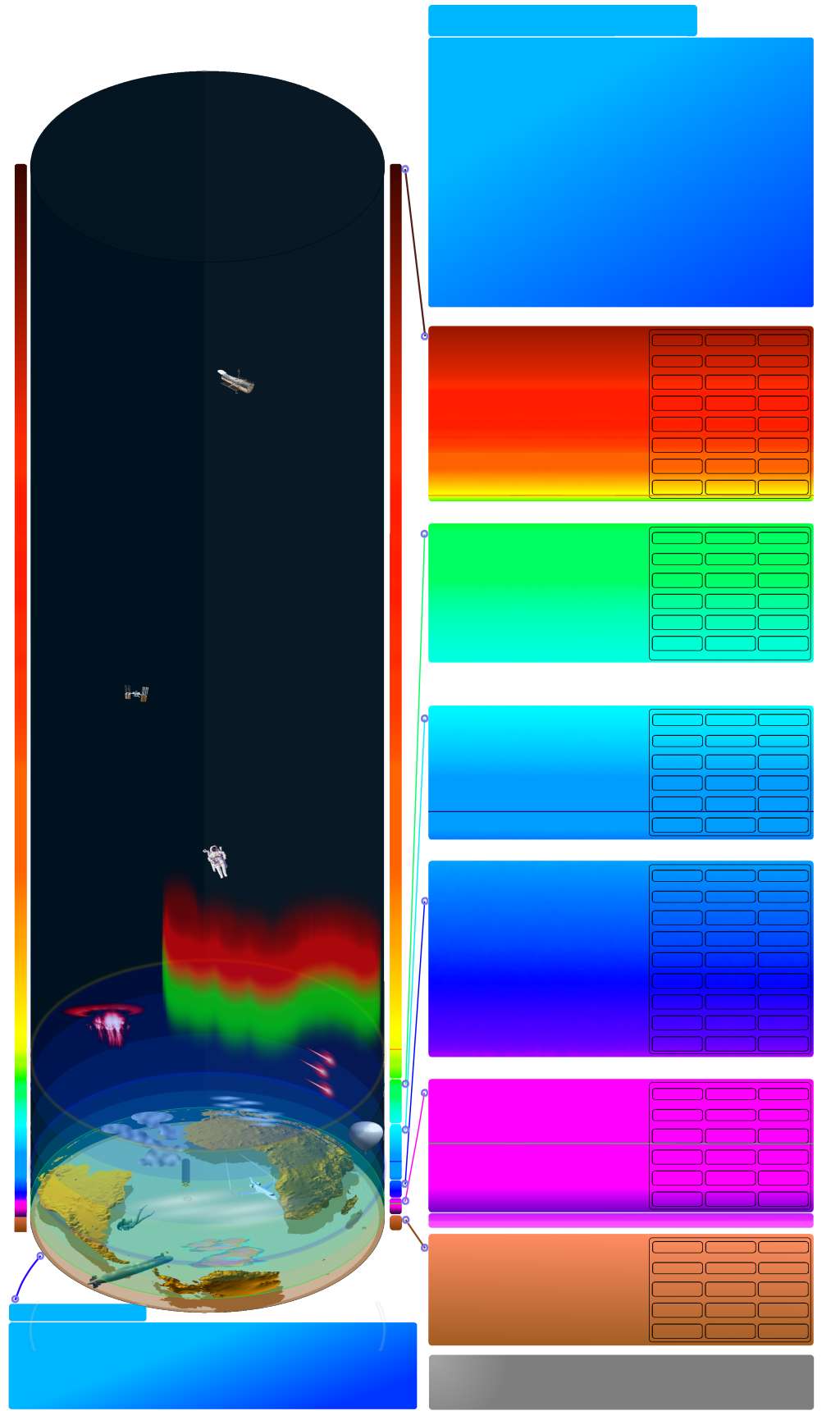
imagens exemplo, sobrepostas usando a predefinição Superimpose2:

commons:File:Column_atmosphere_of_Earth 02.svg

commons:File:Column atmosphere of Earth text pt 02.svg

Para navegar na figura abaixo use a barra de rolagem à direita.

Atmosfera da Terra

Coluna de densidade do ar

Outro exemplo de uso com imagem vertical:

imagem exemplo: commons:File:Elektrownia Siersza 8.jpg

Para navegar na figura abaixo use a barra de rolagem à direita.

Usina de Energia Siersza

Panorâmica em arco das torres de resfriamento de água da Usina de Energia Termoelétrica Siersza, Trzebinia-Polônia

Panorâmica da Usina de Energia Siersza

Exemplo de uso com imagem horizontal:

imagem exemplo: commons:File:Panorama da ferrovia Vitória-Minas em Baixo Guandu.jpg

Para navegar na figura abaixo use a barra de rolagem abaixo.

Ferrovia Vitória-Minas

Panorâmica da ferrovia Vitória-Minas em Baixo Guandu, Brasil

Panorâmica da ferrovia Vitória-Minas em Baixo Guandu, Brasil

Ver também